Question

Please see photo below and answer question two Hello hello hello Answer the question

Answer 1

a.

b.

Explanation:

We have the following functions:

`\begin{gathered} f\mleft(x\mright)=√(x) \\ g\mleft(x\mright)=√(x+4) \\ h\mleft(x\mright)=√(x)+4 \end{gathered}`

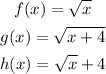
a.

We calculate all the values for each function.

For f(x):

`\begin{gathered} f\mleft(0\mright)=\sqrt[]{0}=0 \\ f(4)=√(4)=2 \\ f(8)=√(8)=2√(2) \\ f(16)=\sqrt[]{16}=4 \end{gathered}`

For g(x):

`\begin{gathered} g\mleft(0\mright)=\sqrt[]{0+4}=\sqrt[]{4}=2 \\ g(4)=\sqrt[]{4+4}=\sqrt[]{8}=2√(2) \\ g(8)=\sqrt[]{8+4}=\sqrt[]{12}=2√(3) \\ g(16)=\sqrt[]{16+4}=\sqrt[]{20}=2√(5) \end{gathered}`

For h(x):

`\begin{gathered} h\mleft(0\mright)=\sqrt[]{0}+4=0+4=4 \\ h(4)=\sqrt[]{4}+4=2+4=6 \\ h(8)=\sqrt[]{8}+4=2√(2)+4 \\ h(16)=\sqrt[]{16}+4=4+4=8 \end{gathered}`

Now, we fill the table with the obtained values:

b.

To graph on the Cartesian plane, what we do is locate the points and then draw the line between these points to obtain the graph, like this: