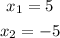Given the Quadratic Equation:
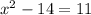
You can solve it as follows:
1. Apply the Addition Property of Equality by adding 14 to both sides of the equation:
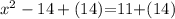
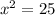
2. By definition, the square root undoes the effect of exponent 2 on the variable. Then, you have to take the square root of both sides of the equation:
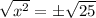
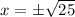
3. Notice that you can split the equations into two equations:
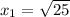
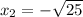
4. Knowing that:
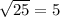
You get:
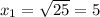
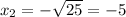
Hence, the answer is: