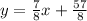
Step-by-step explanation
Step 1
find the slope of the given line
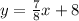
this equation is in the form, slope -intercept

where m is the slope , so
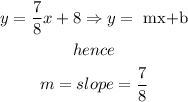
Step 2
2 lines are parallel if the slope is the same,so we are looking for a line with slope 7/8 and the point c(1,8) is part of the line
use
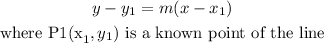
then
Let
P1=C=(1,8)
slope=7/8
now, replace
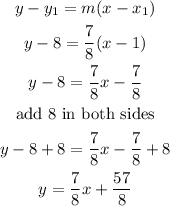
I hope this helps you