Question

Answer question number 17. The question is in the image.

Answer 1

A trigonometric function (sin or cos) can be written as

`g(x)=A\cos(\omega t)\text{ or }g(x)=A\sin(\omega t)`

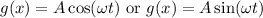
Where A is the amplitude and ω is

`\omega=(2\pi)/(T)`

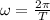
Where T is the period of the function.

Then, let's see the function in 20.

`g(x)=(1)/(2)\cos(4\pi x)`

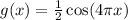
The amplitude of the function 1/2, let's find the period

`\begin{gathered} 4\pi=\omega \\ \\ 4\pi=(2\pi)/(T) \end{gathered}`

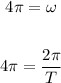
Solve it for T

`\begin{gathered} T=(2\pi)/(4\pi) \\ \\ T=(1)/(2) \end{gathered}`

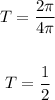
Therefore, the period of the function is 1/2, now we can graph the function, the parent function will be cos(x):

To graph

`g(x)=(1)/(2)\cos(4\pi x)`

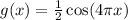
We have to modify the amplitude to 1/2, therefore

Now, we have to modify the period, the function will be period in 1/2, then

Final answer: