The formula used to calculate the total amount at the end of the period is given to be:

where
A = Accrued amount (principal + interest)
P = Principal amount
r = Annual nominal interest rate as a decimal
t = time in decimal years.
From the question, we have the following parameters:
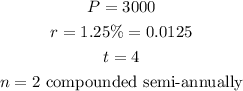
Therefore, we can solve the final amount as follows:
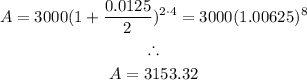
The interest will be calculated to be:
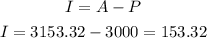
Therefore, the final amount is $3,153.32.
The interest is $153.32.