Solution. B) 7.05 seconds
Analysis: We can use second derivative to find value of t where we would have maximum velocity.
In the first step, let's find first derivative.
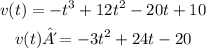
Now, let's find critical points, where the first derivative is equal to zero. We can use quadratic equation:
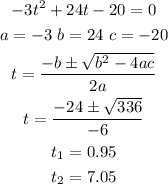
Now, let's find second derivative:

Now, let's replace both critical points in second derivative. If the result is negative, the point is a maximum of the function. If the result is positive, the point is a minimum of the function.
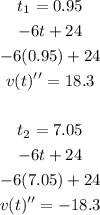
As you can see, when we use t=7.05 the result is negative. So, t=7.05 is a maximum of the function.