Question

Read image for instructions Find the measure of the angle indicated.

Answer 1

Step 1: Theorem

The measure of the angle between two tangent that intercept outside a circle is half the positive difference of the measure of the intercepted arcs.

Step 2: Redraw the figure.

Step 3:

We know that 2x + 240 = 360.

Collect like terms

`\begin{gathered} 2x\text{ + 240 = 360} \\ 2x\text{ = 360 - 240} \\ 2x\text{ = 120} \\ \text{x = }(120)/(2) \\ x\text{ = 60} \end{gathered}`

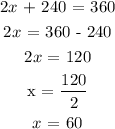
The value of x can also be calculated using the formula below from the theorem.

The measure of the angle between two tangent that intercept outside a circle is half the positive difference of the measure of the intercepted arcs

`\begin{gathered} \text{x = }\frac{240\text{ - 2x}}{2} \\ \text{Cross multiply} \\ 2x\text{ = 240 - 2x} \\ \text{Collect like terms} \\ 2x\text{ + 2x = 240} \\ 4x\text{ = 240} \\ \text{Divide through by 4} \\ (4x)/(4)\text{ = }(240)/(4) \\ \text{x = 60}^o \end{gathered}`