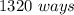Question

First ,second and third-place prizes are to be awarded a dance contest in which 12 contestants are entered. In how many ways can the prizes be awarded?

Answer 1

You know that:

- There are 3 places that are to be awarded: First place, second place, and third place.

- The number of contestants in the dance contest is 12.

Then, you need to use Permutation in order to solve this exercise. Remember that, by definition:

`P(n,r)=\frac{n!^{}}{(n-r)!}`

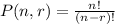
Where "n" is the total number of things to choose from and "r" is the number of things chosen.

In this case, you can identify that:

`\begin{gathered} n=12 \\ r=3 \end{gathered}`

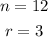
Then, substituting and evaluating, you get:

`P(12,3)=\frac{12!^{}}{(12-3)!}=(12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)/(9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)`
`=(479001600)/(362880)=1320`

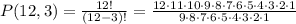
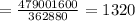
Therefore, the answer is:

`1320\text{ }ways`