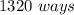You know that:
- There are 3 places that are to be awarded: First place, second place, and third place.
- The number of contestants in the dance contest is 12.
Then, you need to use Permutation in order to solve this exercise. Remember that, by definition:
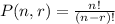
Where "n" is the total number of things to choose from and "r" is the number of things chosen.
In this case, you can identify that:
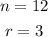
Then, substituting and evaluating, you get:
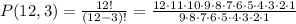
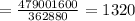
Therefore, the answer is: