Question

Consider these functions:【二=16=2(a)=毫任For x2 0, the value of Rebo) isFor x2 0, the value of gl f(x)) isFor x2 0, functions fand e

Answer 1

Given: Two functions as follows

`\begin{gathered} f(x)=16x^2 \\ g(x)=(1)/(4)√(x) \end{gathered}`

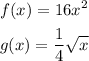
Required: To find f(g(x)) and g(f(x)).

Explanation: f(g(x)) can be determined by putting g(x) in f(x) as follows

`f(g(x))=16[g(x)]^2`
`\begin{gathered} f(g(x))=16((1)/(4)√(x))^2 \\ =16*(x)/(16) \\ =x \end{gathered}`

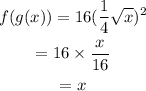
Similarly, for g(f(x)) we have

`g(f(x))=(1)/(4)(√(16x^2))`
`\begin{gathered} =(1)/(4)*4x \\ =x \end{gathered}`

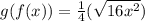
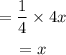
Since. f(g(x))=g(f(x)) the given functions f(x) and g(x) are inverse.

Final Answer: a) f(g(x)) is x

b) g(f(x)) is x

c) Functions f and g are inverse functions.