Let's use the variable "A" to represent the number of adult tickets and "S" to represent the number of senior tickets.
If each adult ticket is $11, each senior ticket is $10, and the total ticket sales were $4,286, we can write the following equation:
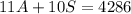
Also, if the number of senior tickets sold was 24 less than twice the number of adult tickets, we can write the following equation:
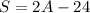
Using this value of S in the first equation, we have that:

Now, finding the value of S, we have:
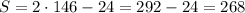
So the number of tickets sold is 146 adult tickets and 268 senior tickets.