A bear population is increasing by 5% each year. This year, there 43 bears. How many bears will there be next year? Round your answer to the nearest whole number.

Question

asked May 3, 2023 173k views

1 Answer

OddBeck · Answer 1 · 2023-05-07T01:41:20+0000

Exponential Growth

If a population has exponential growth, starting from an initial population Po, then the future number of members of the population is given by:

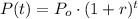
$P(t)=P_o\cdot(1+r)^t$

Where r is the growth rate and t is the time.

We are given the current population of bears Po = 43 and the increasing rate of r = 5% = 0.05 each year, thus the model can be written as:

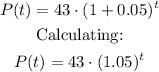
$\begin{gathered} P(t)=43\cdot(1+0.05)^t \\ \text{Calculating:} \\ P(t)=43\cdot(1.05)^t \end{gathered}$

Next year (t = 1), the population is expected to be:

$\begin{gathered} P(1)=43\cdot(1.05)^1 \\ P(1)=43\cdot(1.05) \\ P(1)\approx45 \end{gathered}$

There will be 45 bears next year