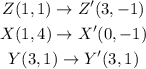1.
A rotation of 90° clockwise about the origin will make the figure swap its x and y coordinates. Also, the figure will go from the 1st quadrant to the 4th quadrant, so its y-coordinates will be negative.
So we have:
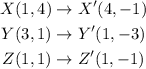
2.
A rotation of 180° about point Z will make the y-coordinate of point X decrease by 6 units (double the length of XZ) and the x-coordinate of point Y will decrease by 4 units (double the length of YZ). Point Z will be in the same location. So we have:
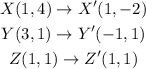
3.
A rotation of 90° ccw about point Y will make the segment YZ point downwards, so the x-coordinate of Z increases by 2 and its y-coordinate decrease by 2.
The segment ZX will point to the left, so the x-coordinate of X will be the x-coordinate of Z' minus 3, and its y-coordinate will be the same as the y-coordinate of Z'.
Y' is in the same location of Y: