Question

X+7 less than or equal to -2 or x+7 greater than or equal to -3

Answer 1

`-10\le x\le-9`

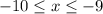
Explanations:

Given the following inequality expressions:

`x+7\leq-2\text{ or }x+7\ge-3`

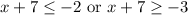
The inequality expression x + 7 ≥ - 3 can be written as -3 ≤ x + 7.

Combine -3 ≤ x + 7 with x + 7 ≤ -2 to have:

`-3\leq x+7\leq-2`

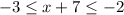
Subtract 7 from all the sides to have:

`\begin{gathered} -3-7\leq x+7-7\leq-2-7 \\ -10\leq x\leq-9 \end{gathered}`

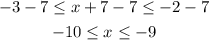
Hence the solution to the system of inequalities is -10 ≤ x ≤ -9