Let x be the number of hours Gavin works as lifeguarding and y be the number of hours he works walking dogs, then we can set the following system of inequalities:
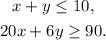
Solving the first inequality for y, we get:
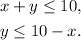
Solving the second inequality for y we get:
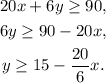
Answer: Inequality 1
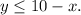
Inequality 2
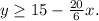
Now, to find a solution we overlap the above graphs:
A possible solution is x=5 and y=4.