Question

Gavin is working two summer jobs, making $20 per hour lifeguarding and making $6per hour walking dogs. In a given week, he can work no more than 10 total hours andmust earn at least $go. If a represents the number of hours lifeguarding and yrepresents the number of hours walking dogs, write and solve a system of in qualitiesgraphically and determine one possible solution.

Answer 1

Let x be the number of hours Gavin works as lifeguarding and y be the number of hours he works walking dogs, then we can set the following system of inequalities:

`\begin{gathered} x+y\le10, \\ 20x+6y\ge90. \end{gathered}`

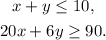
Solving the first inequality for y, we get:

`\begin{gathered} x+y\le10, \\ y\le10-x\text{.} \end{gathered}`

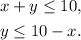
Solving the second inequality for y we get:

`\begin{gathered} 20x+6y\ge90, \\ 6y\ge90-20x, \\ y\ge15-(20)/(6)x\text{.} \end{gathered}`

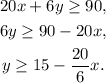
Answer: Inequality 1

`y\le10-x\text{.}`

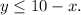
Inequality 2

`y\ge15-(20)/(6)x_{}\text{.}`

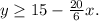
Now, to find a solution we overlap the above graphs:

A possible solution is x=5 and y=4.