Question

A motorboat travels 165 kilometers in 3 hours going upstream and 465 kilometers in 5 hours going downstream. What is the rate of the boat in still water and what is the rate of the current?

Answer 1

Answer: The rate of the boat in still water is 74 km/hr ,and the rate of the current is 19 km/hr

Step-by-step explanation:

Let:

x= the speed of the boat

y=the speed of the stream

Then,

x-y = the speed upstream

x+y = the speed downstream

So, the upstream speed is:

and, the downstream speed is:

`\begin{gathered} x+y=(465)/(5) \\ x+y=93 \end{gathered}`

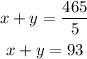
To find the value of x and y, we use the following equations:

x-y= 55

x+y=93

Then, solve for x in x-y =55.

x=55 +y

Substitute x=55 + y into x+y=93.

x+y=93

(55 +y) + y=93

55+2y = 93

`\begin{gathered} \text{Simplify and rearrange} \\ 2y=93-55 \\ 2y=38 \\ y=(38)/(2) \\ \text{Calculate} \\ y=19 \end{gathered}`

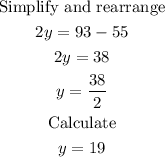
Substitute y=19 into x+y = 93.

x+y= 93

x+ 19 =93

Simplify and rearrange

x=93-19

Calculate

x=74

Therefore, the rate of the boat in still water is 74 km/hr ,and the rate of the current is 19 km/hr.