Question

You are designing a Quincke's tube to demonstrate the phenomenon of acoustic interference. The sine wave to be played by a speaker into the end of the tube will have a frequency of 344Hz. The shorter tube has a length of one meter. How long does the longer tube have to be so that the waves traveling down each tube destructively interfere when they meet?

Answer 1

Given data:

* The length of the shorter tube is,

`l_1=1\text{ m}`

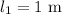
* The frequency of the wave is,

`f=344\text{ Hz}`

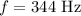
Solution:

As the speed of sound wave is 340 m/s

Thus, the wavelengh of the wave is,

`\lambda=(v)/(f)`

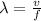
where v is the speed of sound wave, and f is the frequency of the wave,

Substituting the known values,

`\begin{gathered} \lambda=(340)/(344) \\ \lambda=0.988\text{ m} \end{gathered}`

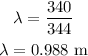
For the destructive interference,

The path difference between the waves for the first order minima is,