Given data:
* The length of the shorter tube is,
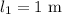
* The frequency of the wave is,
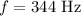
Solution:
As the speed of sound wave is 340 m/s
Thus, the wavelengh of the wave is,
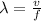
where v is the speed of sound wave, and f is the frequency of the wave,
Substituting the known values,
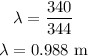
For the destructive interference,
The path difference between the waves for the first order minima is,
![undefined]()