Question

-6>x^2+4xSolve the inequality algebraically

Answer 1

Given:

The inequality is given as,

`-6>x^2+4x`

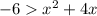
The objective is to solve the inequality algebraically.

Step-by-step explanation:

By adding +4 on both sides of the equation,

`4-6>x^2+4x+4`

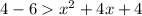
Now, by rearranging the above equation,

`-2>x^2+2(2)x+2^2`

Using algebraic identity,

`-2>(x+2)^2\text{ . . . . . (1)}`

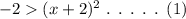
If n is even in a term aⁿ, then the value of the term must be greater than zero.

By consider the equation (1), the degree is 2 in the term (x+2)², then the term must be greater than zero. But the inequality represents that the value is lesser than -2.

Hence, the given inequality has no solution.