Question

Find the number of ways to arrange the letters in GIGGLE

Answer 1

There are 6 letters in the words GIGGLE, to be able to find the number of ways to arrange the letters, we will be using the Permutation Formula:

`\text{ P(n,r) = }\frac{\text{ n!}}{\text{ (n - r)!}}`

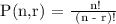
Where,

n = total number of objects in the set = number of letters in GIGGLE = 6

r = number of choosing objects from the set = be arranged in 6 letters still = 6

We get,

`\text{ P(n,r) = }\frac{\text{ n!}}{\text{ (n - r)!}}`
`\text{ P(6,6) = }\frac{\text{ 6!}}{\text{ (6 - 6)!}}`
`\text{ P(6,6) = 6 x 5 x 4 x 3 x 2 x 1}`
`\text{ P(6,6) = }720`

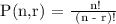
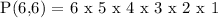
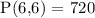
Therefore, there 720 ways to arrange the letters in GIGGLE.

The answer is 720.