SOLUTION
We will apply the formula
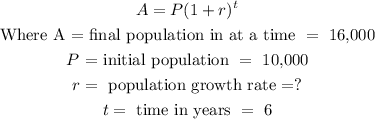
So, before we can find the expected population in the next 4 years, we need to find the population growth rate r,
Now substituting the values above into the equation we have
![\begin{gathered} A=P(1+r)^t \\ 16,000=10,000(1+r)^6 \\ (1+r)^6=(16,000)/(10,000) \\ (1+r)^6=1.6 \\ \text{taking the 6th root of both sides } \\ \sqrt[6]{(1+r)^6}=\sqrt[6]{1.6} \\ 1+r=1.081484 \\ r=1.081484-1 \\ r=0.081484 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aw07jlwzkn7t6or0rizffx7g1nph9xh1k0.png)
So, we have found the rate, which is about 8.15%,
Now, the expected population in 4 years becomes
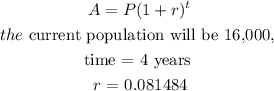
Substituting the values, we have
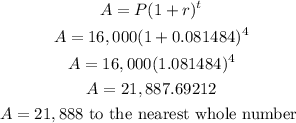
Hence, the answer is 21,888 to the nearest whole number