Question

state whether the product of
`√(3)`and
`√(9)`is rational or irrational explain your answer .

Answer 1

`√(3)*√(9)=√(3*9)=√(27)`

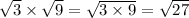
Let us simplify the root

In the square root, if a number under it repeated twice, it will go out the root

EX:

`√(4)=√(2*2)`

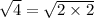
Since 2 is repeated twice, then it will go out the root so the answer will be 2

`√(4)=2`
`√(8)=√(2*2*2)=2√(2)`

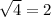
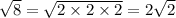
Since 2 is repeated three times two of them will go out the root and one will be under the root

That means to simplify the square root, factorize the number using prime numbers and any number repeated twice takes it out the root

Let us solve the question

`√(27)=√(3*3*3)`

Take two 3 out and leave one under the root

`√(27)=3√(3)=5.196152423`

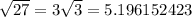
Since this value is approximated value, so

The product is an irrational number

The rational number are the numbers you can put them in the form of a fraction

EX: 2, 12.5, 22/7, 100, square root 64 (because it is equal 8), 0.23, .....

The irrational numbers are the numbers you can not put it in the form of the fraction like any approximated number

EX:

`√(5)\text{ , }\pi,\sqrt[,3]{7},\ldots\ldots`

The product is

`3√(3)`

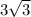
It is an irrational number

Because it gives you approximated value