A true equiation has a real solution, for example

is true equation because you can find the value of x
multiply X to both sides
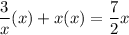
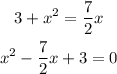
and you can factorize and solve

It has two solutions for x
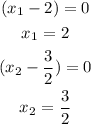
and a false equation has not solution or is not real, for example
![\sqrt[]{x}=-2](https://img.qammunity.org/2023/formulas/mathematics/college/2oqwlsf4ek8gxtc9o67o2cqfzq12dhap7f.png)
this cant not be, because when you try to solve x you have:
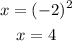
but when you replace to check equality
![\begin{gathered} \sqrt[]{(4)}=-2 \\ 2\\e-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w2tzvf7favnb07dpq7x2xcrg5hurv0kvua.png)