To calculate the angle through which wheel B rotates, we need to find the length through which wheel A travels at 180°.
We are given
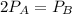
We can calculate the perimeter of the wheel as
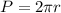
If
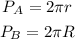
we will have

The length travelled by wheel A in 180° is given as
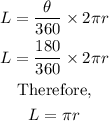
Since wheel B will travel the same length as wheel A, we can write out the expression as
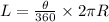
Putting the value of L and R as gotten above, we have

Dividing through by πr and solving for θ, we have
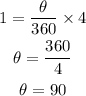
The wheel B is rotated 90°.