Question

Wheel A has half the perimeter of wheel B. if Wheel A is rotated 180°, how many degrees is wheel B rotated?

Answer 1

To calculate the angle through which wheel B rotates, we need to find the length through which wheel A travels at 180°.

We are given

`2P_A=P_B`

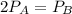
We can calculate the perimeter of the wheel as

`P=2\pi r`

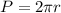
If

`\begin{gathered} P_A=2\pi r \\ P_B=2\pi R \end{gathered}`

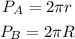
we will have

`\begin{gathered} 2(2\pi r)=2\pi R \\ 4\pi r=2\pi R \\ \text{Therefore} \\ R=2r \end{gathered}`

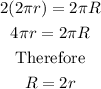
The length travelled by wheel A in 180° is given as

`\begin{gathered} L=(\theta)/(360)*2\pi r \\ L=(180)/(360)*2\pi r \\ \text{Therefore,} \\ L=\pi r \end{gathered}`

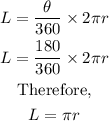
Since wheel B will travel the same length as wheel A, we can write out the expression as

`L=(\theta)/(360)*2\pi R`

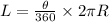
Putting the value of L and R as gotten above, we have

`\pi r=(\theta)/(360)*2*\pi*2r`

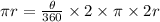
Dividing through by πr and solving for θ, we have

`\begin{gathered} 1=(\theta)/(360)*4 \\ \theta=(360)/(4) \\ \theta=90 \end{gathered}`

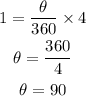
The wheel B is rotated 90°.