The first plan charges 20 cents per minute
Since 1 dollar = 100 cents, then
20/100 = 0.20 dollars
The first plan charges $0.20 per minute
The second plan charges $39.95 plus 10 cents per minute
10/100 = 0.10 dollars
The second plan charges $39.95 plus $0.10 per minute
We need to make the 2nd plan preferable
That means the charge for the 2nd less than the 1st charge
Let the number of minutes = x, then
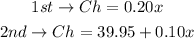
We will make 2nd Ch < 1st Ch
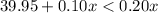
Subtract 0.10x from both sides

Divide both sides by 0.10

Since the first whole number greater than 399.5 is 400
Then x = 400
You would have to use the 2nd plan for 400 minutes to be preferable