Question

A nutritionist claims that the mean tuna consumption by a person is 3.5 pounds per year. Asample of 80 people shows that the mean tuna consumption by a person is 3.2 pounds peryear. Assume the population standard deviation is 1.22 pounds. At a= 0.07, can you reject theclaim?Identify the null hypothesis and alternative hypothesis

Answer 1

Here is what we know:

Sample size: 80 people

Mean consumption by a person from the sample: 3.2 pounds

Sample standard deviation: 1.22 pounds

Tuna consumption according to the nutritionist claims: 3.5 pounds

Alpha: 0.07

First, we compute the standard deviation of the mean:

`\sigma_(\mu)=(\sigma)/(√(n))=(1.22)/(√(80))\approx0.136\text{ pounds}`

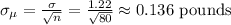
Then, the z score for the nutritionist claims is given by:

`Z=(x-\mu)/(\sigma_(\mu))=(3.5-3.2)/(0.136)\approx2.2`

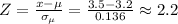
Then, according to a normal table, we have:

`P(Z\ge2.2)+P(Z\leq2.2)=2\cdot(0.5-0.4861)=0.0278`

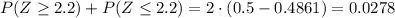
We can check that 0.0278 < 0.07, therefore the null hypothesis, is rejected.

The null hypothesis is given by:

`\begin{gathered} P(z\leq Z_(null))+P(z\ge Z_(null))\ge1-0.07=0.93 \\ According\text{ to the normal table: }Z_(null)=\pm1.81 \\ =(x_(null)-\mu)/(\sigma_(\mu)) \\ \pm1.81=(x_(null)-3.2)/(0.136) \\ x_(null)=3.2\pm1.81\cdot0.136\approx3.2\pm0.25 \\ null\text{ hypothesis: 2.95}\leq x\text{ }\leq\text{ 3.45} \\ Alternative\text{ hypothesis: }x\leq2.95\text{ or }x\ge3.45 \end{gathered}`

Null hypothesis: 2.95 <= x <= 3.45

Alternative hypothesis: x <= 2.95 or x >= 3.45