Given: The function below
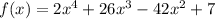
To Determine: The interval of the inflection points
Solution:
The inflection points is the point where the second derivative of the function is equal to zero
Step 1: Determine the first derivative
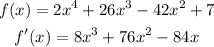
Step 2: Determine the second derivative
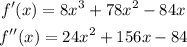
Step 3: Equate the second derivative to zero
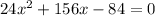
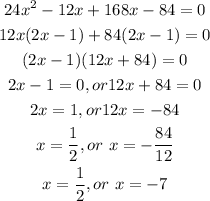
![undefined]()