For this problem we can start estimating the area for the 8 people
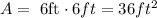
And we also know that 8 people fit on this area
Then we can find the total area for the new structure (A1) but first we need to convert first 2yd to ft and 3 mi to ft, we know that:
1 yd= 3ft and 1 mi = 5280 ft.
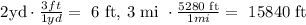
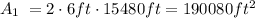
And then we can use a proportional rule given by:
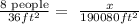
And solving for x we got:
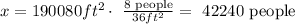
And for this case the final answer would be 42240 people