Givens.
• Time = 0.64 s.
,
• Tangential speed = 1.02 m/s.
The period is 0.64 seconds per revolution.
Then, we use the following formula.
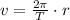
Where v = 1.02 m/s and T = 0.64 seconds. Solve for r.
![\begin{gathered} r=(v\cdot T)/(2\pi) \\ r=(1.02\cdot(m)/(s)\cdot0.64s)/(2\pi) \\ r=(0.6528)/(2\pi)m \\ r\approx0.104m=10.4\operatorname{cm} \end{gathered}]()
Therefore, the radius is 10.4 cm.
If the radius were 0.05 meters but using the same period, the tangential speed would be
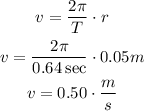
The tangential speed would be 0.50 meters per second, which is faster than the tangential speed with a larger radius.