Question

It takes a time t = 0.64 s for a record to revolve on a record player once. A particular point on the record moves past the needle at a speed of vn = 1.02 m/s. what is the raduis at which the needle is incontact with the record?

Answer 1

The radius at which the needle is in contact with the record is approximately 0.104 m.

Step-by-step explanation:

To find the radius at which the needle is in contact with the record, we need to use the formula for linear velocity in uniform circular motion. The linear velocity is given by the formula v = rω, where v is the linear velocity, r is the radius, and ω is the angular velocity. In this case, the linear velocity is 1.02 m/s and the time for one revolution is 0.64 s. Rearranging the formula, we have r = v/ω. The angular velocity is given by the formula ω = 2π/T, where T is the period of one revolution. Substituting the values, we get ω = 2π/0.64, which is approximately 9.82 rad/s. Now we can substitute the values into the formula for radius, r = 1.02/9.82. Calculating this, we get a radius of approximately 0.104 m.

Answer 2

Givens.

• Time = 0.64 s.

,

• Tangential speed = 1.02 m/s.

The period is 0.64 seconds per revolution.

Then, we use the following formula.

`v=(2\pi)/(T)\cdot r`

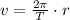
Where v = 1.02 m/s and T = 0.64 seconds. Solve for r.

Therefore, the radius is 10.4 cm.

If the radius were 0.05 meters but using the same period, the tangential speed would be

`\begin{gathered} v=(2\pi)/(T)\cdot r \\ v=(2\pi)/(0.64\sec)\cdot0.05m \\ v=0.50\cdot(m)/(s) \end{gathered}`

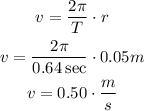
The tangential speed would be 0.50 meters per second, which is faster than the tangential speed with a larger radius.