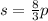Let be "x" the number of bottles of sparkling water that the company produces when it produces 600 bottles of plain water.
a. You know that the factory produces 3 bottles of sparkling water for every 8 bottles of plain water.
Therefore, knowing that it produces 600 bottles of plain water, you can write the following proportion:

Solve for "s" :
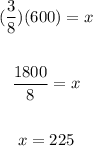
b. Knowing that the ratio is:
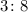
You can set up the following equation:
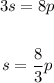
Where "s" is the number of bottles of sparkling and "p" is the number of bottles of plain water.
Therefore, the answers are:
a. 225 bottles of sparkling water.
b.