Question

An aquarium tank can hold 6000 liters of water. There are two pipes that can be used to fill the tank. The first pipe alone can fill the tank in 75 minutes. The second pipe can fill the tank in 50 minutes by itself. When both pipes are working together, how long does it take them to fill the tank?

Answer 1

We will have the following:

First, we determine the rate of filling for each pipe as follows:

`\begin{cases}p_1=(6000l)/(75\min)\Rightarrow p_1=(80l)/(\min) \\ \\ p_2=(6000l)/(50\min)\Rightarrow p_2=(120l)/(\min )\end{cases}`

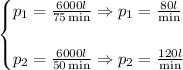
So, the first pipe fills it at a rate of 80 liters per minute and the second one at a rate of 120 liters per minute.

Now, we determine the time it would take to fill it for the two rates combined, that is:

`p_3=p_1+p_2\Rightarrow p_3=(200l)/(\min )`

So:

`x=(6000l\cdot1\min)/(200l)\Rightarrow x=30\min`

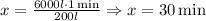
So, it will take 30 minutes to be filled by both pipes at the same time.