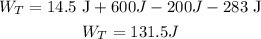Given
m = 6kg
x = 8m
F = 75 N
vo = 2.2 m/s up
Ff = 25 N
Procedure
(a) Initial kinetic energy of the block
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity.
![\begin{gathered} K=(1)/(2)mv^2 \\ K=(1)/(2)6\operatorname{kg}\cdot(2.2m/s)^2 \\ K=14.5\text{ J} \end{gathered}]()
(b) the work done by the 75N force;
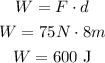
(c) the work done by the friction force
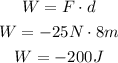
(d) the work done by gravity
![\begin{gathered} W=\text{mg}\cdot d\cdot\sin (37) \\ W=6\operatorname{kg}\cdot9.8m/s^2\cdot8m\cdot\sin (37) \\ W=-283\text{ J} \end{gathered}]()
(e) the work done by the normal force
0J, perpendicular force to the motion
(f) the final kinetic energy of the block.