Question

The area of a rectangle is 65 m², and the length of the rectangle is 3 m less than twice the width. Find the dimensions of the rectangle.What is length and width

Answer 1

Step-by-step explanation

Let the length be l and width b W, Since the length of the rectangle is 3 m less than twice the width, we will have

`L=2w-3`

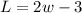
Therefore, the area becomes

`\begin{gathered} A=l* w \\ 65=w(2w-3) \\ 65=2w^2-3w \\ 2w^2-3w-65=0 \\ \mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:} \\ x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a) \\ \mathrm{For\:}\quad a=2,\:b=-3,\:c=-65 \\ w_(1,\:2)=(-\left(-3\right)\pm √(\left(-3\right)^2-4\cdot \:2\left(-65\right)))/(2\cdot \:2) \\ \mathrm{Separate\:the\:solutions} \\ w_1=(-\left(-3\right)+23)/(2\cdot \:2),\:w_2=(-\left(-3\right)-23)/(2\cdot \:2) \\ \mathrm{The\:solutions\:to\:the\:quadratic\:equation\:are:} \\ w=(13)/(2),\:w=-5 \end{gathered}`

Logically, the width becomes

Answer: width = 6.5m

Therefore, the length becomes

`l=2w-3=2(6.5)-3=13-3=10`

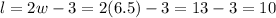
Answer" lenght =10 m