Given the following information,
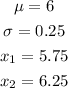
Given the formula for the z-score below,
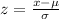
To find the z-score of the worker's wage for x₁
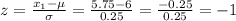
To find the z-score of the worker's wage for x₂,
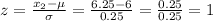
By the empirical rule, 68-95-99.7% of the z-score lies within the normal distribution of the worker's wage between $5.75 and $6.25 hence, the probability is 0.68.