Question

For certain workers, the mean wage is $6.00/hr, with a standard deviation of $0.25. If a worker is chosen at random, what is the probability that the worker's wage is between $5.75 and $6.25? Assume a normal distribution of wages.

Answer 1

Given the following information,

`\begin{gathered} \mu=6 \\ \sigma=0.25 \\ x_1=5.75 \\ x_2=6.25 \end{gathered}`

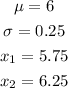
Given the formula for the z-score below,

`z=(x-\mu)/(\sigma)`

To find the z-score of the worker's wage for x₁

`z=(x_1-\mu)/(\sigma)=(5.75-6)/(0.25)=(-0.25)/(0.25)=-1`

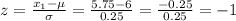
To find the z-score of the worker's wage for x₂,

`z=(x_2-\mu)/(\sigma)=(6.25-6)/(0.25)=(0.25)/(0.25)=1`

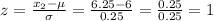
By the empirical rule, 68-95-99.7% of the z-score lies within the normal distribution of the worker's wage between $5.75 and $6.25 hence, the probability is 0.68.