Let the number of children attended be c;
Let the number of adults attended be a;
and let the number of students that attended be s;
Then;
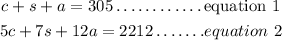
But there are half as many adults as there are children, then;
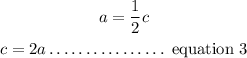
By substituting equation 3 in equation 1 and equation 2, we have;
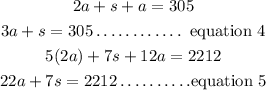
Solving equation 4 and equation 5 simultaneously, we have;

Then, we substitute the value of a and s in equation 1 to get the value of c;
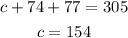
154 children attended
74 students attended
77 adults attended.