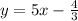The slope formula for tow given points is

where, in our case,
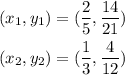
By substituting these values into our formula, we have
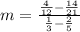
Lets compute the numerator first. We have
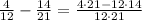
which gives
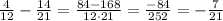
Similarly, in the denominator we have
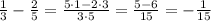
Then, our slope is given by
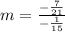
By applying the sandwhich law, we get
then, the slope is m=5. Then, our line has the followin form
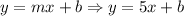
where b is the y-intercept. We can find b by substituting one of the 2 given points, that is, if we substitute point (1/3,4,12) into the last expression, we have
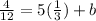
which gives
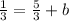
then b is given by
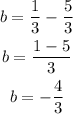
And finally, the line equation in slope-intercept form is