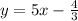Question

What is the equation of the line passing through the points (2/5. (14/21) and (1/3) . (4/12) slope intercept form?

Answer 1

The slope formula for tow given points is

`m=(y_2-y_1)/(x_2-x_1)`

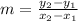
where, in our case,

`\begin{gathered} (x_1,y_1)=((2)/(5),(14)/(21)) \\ (x_2,y_2)=((1)/(3),(4)/(12)) \end{gathered}`

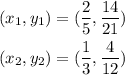
By substituting these values into our formula, we have

`m=((4)/(12)-(14)/(21))/((1)/(3)-(2)/(5))`

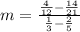
Lets compute the numerator first. We have

`(4)/(12)-(14)/(21)=(4\cdot21-12\cdot14)/(12\cdot21)`

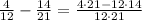
which gives

`(4)/(12)-(14)/(21)=(84-168)/(12\cdot21)=(-84)/(252)=-(7)/(21)`

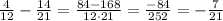
Similarly, in the denominator we have

`(1)/(3)-(2)/(5)=(5\cdot1-2\cdot3)/(3\cdot5)=(5-6)/(15)=-(1)/(15)`

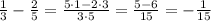
Then, our slope is given by

`m=(-(7)/(21))/(-(1)/(15))`

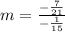
By applying the sandwhich law, we get

then, the slope is m=5. Then, our line has the followin form

`y=mx+b\Rightarrow y=5x+b`

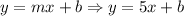
where b is the y-intercept. We can find b by substituting one of the 2 given points, that is, if we substitute point (1/3,4,12) into the last expression, we have

`(4)/(12)=5((1)/(3))+b`

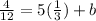
which gives

`(1)/(3)=(5)/(3)+b`

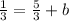
then b is given by

`\begin{gathered} b=(1)/(3)-(5)/(3) \\ b=(1-5)/(3) \\ b=-(4)/(3) \end{gathered}`

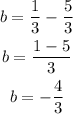
And finally, the line equation in slope-intercept form is

`y=5x-(4)/(3)`