Question

In △ABC,a=13, b=14, and c=18. Find m∠A.A. 49.3B. 48.2C. 45.9D. 39.5

Answer 1

Answer:C. 45.9Explanation:

The given diagram is a triangle. In order to get the angle m∠A, we will use the cosine rule as shown below:

`a^2=b^2+c^2-2bc\cos m\angle A`

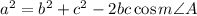
Given the following:

a = 13

b = 14

c = 18

Substitute the given parameters into the formula:

`\begin{gathered} 13^2=14^2+18^2-2(14)(18)\cos m\angle A \\ 169=196+324-504\cos m\angle A \\ 169=520-504\cos m\angle A \\ 169-520=-504\cos m\angle A \\ -351=-504\cos m\angle A \\ \cos m\angle A=(-351)/(-504) \\ \cos m\angle A=(351)/(504) \\ \cos m\angle A=0.6964 \\ m\angle A=\cos ^(-1)0.6964 \\ m\angle A=45.85 \\ m\angle A\approx45.9^0 \end{gathered}`

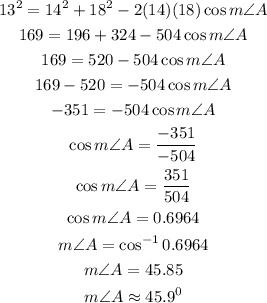
This shows that option C is correct.