A quadratic function can be given as follows:
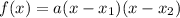
where x1 and x2 are the zeros of the equation, which means that the equation is given by:
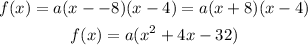
Because the point (-2, 18) is part of the function, we can substitute it, and isolate a to find its value:
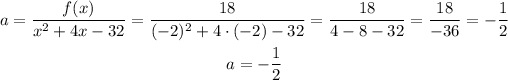
From the solution developed above, we are able to conclude that the answer for the present problem is:
B. -1/2