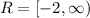Question

find the axis of symmetry and vertex. f(x)=2x2-8x+6. Also find the domain and the range of the function

Answer 1

To find the vertex and axis of simmetry we need to complete the squared on the function:

`\begin{gathered} y=2x^2-8x+6 \\ y=2(x^2-4x)+6 \\ y=2(x^2-4x+(-2)^2)+6-2(-2)^2 \\ y=2(x-2)^2+6-8 \\ y=2(x-2)^2-2 \end{gathered}`

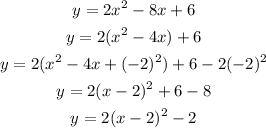
Now the function is written in the form:

`y=a(x-h)^2+k`

in this form the vertex is (h,k). Comparing the equations we conclude that the vertex is at the point (2,-2).

Now, the axis of symmetry on a vertical parabola has the form:

`x=k`

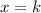
Therefore, the axis of symmetry is:

`x=2`

To graph the function we need to find points on it:

Now we plot this points on the plane and join them with a smooth line:

From the graph we notice that the domain is:

`D=(-\infty,\infty)`

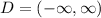
and the range is:

`R=\lbrack-2,\infty)`