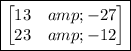In this problem, we want to multiply two matrices together.
First, we need to make sure the matrices are compatible. In general, here is the rule we want to apply:
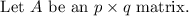
If we want to multiply A to another matrix, then the second matrix must have dimensions
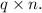
In other words, the number of columns in Matrix A must be equal to the number of rows in the second matrix.
We are given two matrices with the following dimensions:
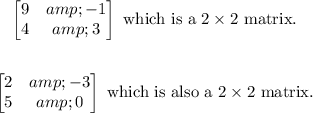
Since the number of columns in the first matrix matches the number of rows in the second matrix, we can complete this multiplication.
When multiplying two matrices, we have to follow a specific algorithm. We'll do this one step at a time to get each element in the final product.
We want to multiply
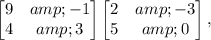
So we will multiply the elements of row 1 in the first matrix, to column 1 in the second matrix:
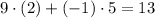
Our matrix now looks like this:
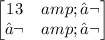
Next, we will multiply the row 1 of the first matrix to column 2 of the second matrix:
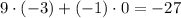
Our matrix looks like:
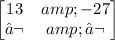
Multiply row 2 of the first matrix to column 1 of the second matrix:
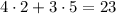
Which gives us
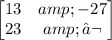
Finally, we multiply row 2 of the first matrix by column 2 of the second matrix:
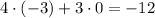
Our final matrix is