Question

Find the values of x and y when the smaller triangle has an area of 42 cm?cm.The value of x is cm and the value of y is a(Type exact answers, using radicals as needed. Rationalize all denominators.)

Answer 1

Given two similar triangles

The corresponding sides are proportions

So,

`(x)/(y)=(24)/(42)=(4)/(7)`

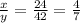
So, the relation between x and y will be:

`x=(4)/(7)y`

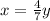
The area of the smaller triangle = 42 cm^2

So, area =

`(1)/(2)x\cdot y=42`

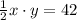
Substitute with x into the equation of the area to find the value of y

`\begin{gathered} (1)/(2)\cdot(4)/(7)y\cdot y=42 \\ \\ y^2=(42\cdot2\cdot7)/(4)=(588)/(4)=147 \\ y=\sqrt[]{147} \end{gathered}`

Substitute with y into x

`x=(4)/(7)\cdot\sqrt[]{147}=\frac{4\sqrt[]{147}}{7}`

So, the answer will be:

`\begin{gathered} x=\frac{4\sqrt[]{147}}{7} \\ \\ y=\sqrt[]{147} \end{gathered}`