Given two similar triangles
The corresponding sides are proportions
So,
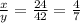
So, the relation between x and y will be:
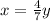
The area of the smaller triangle = 42 cm^2
So, area =
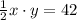
Substitute with x into the equation of the area to find the value of y
![\begin{gathered} (1)/(2)\cdot(4)/(7)y\cdot y=42 \\ \\ y^2=(42\cdot2\cdot7)/(4)=(588)/(4)=147 \\ y=\sqrt[]{147} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m98dikan103x6p44x1vjxlx9xke02rcxm3.png)
Substitute with y into x
![x=(4)/(7)\cdot\sqrt[]{147}=\frac{4\sqrt[]{147}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/x5b1721bj01avocqoyq86ckora9oit6zxv.png)
So, the answer will be:
![\begin{gathered} x=\frac{4\sqrt[]{147}}{7} \\ \\ y=\sqrt[]{147} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mu83svma0ioma7l4xkm5ivi614qf0u49sj.png)