To find the rise (DISTANCE IN Y) of the triangle CDE you use the coordinates in y for the points E and D.
E (11,5) y=5
D (11,-7) y= -7
The rise is:
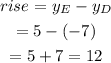
Then, the rise of the given traingle is 12
The run (distance in x) of the triangle CDE is:
C (-10,-7) x=-10
D (11,-7) x=11
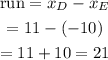
Then, the run of the given triangle is 21
The rate is:
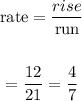
Then, the rate of the given triangle is 4/7