Given:
The length of the wire is,
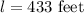
The diameter of the wire is,
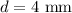
The resistance of the wire is,
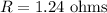
To find:
The length of the wire whose resistance is,
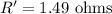
diameter is,
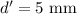
Step-by-step explanation:
The resistance of a conductor is,
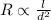
We can write,
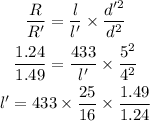
The length is,
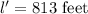
Hence, the required length is 813 feet.