Question

Use the formula for compound amount to find the interest amount:$12,000 at 8% compounded annually for 4 years

Answer 1

The formula to be using is as follows:

`A=P(1+(r)/(n))^(nt)`

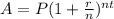
But A is the total amount, that is, the initial amount plus the interest amount. If we want just theinterest, I, we need to substract the initial amount:

`\begin{gathered} I=A-P \\ I=P(1+(r)/(n))^(nt)-P \end{gathered}`

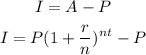
The given information are:

`\begin{gathered} P=12000 \\ r=0.08 \\ n=1 \\ t=4 \end{gathered}`

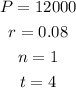
Where r was converted from percentage to decimal and n is 1 because it is compounded only once per year.

So, substituting these values, we have:

`\begin{gathered} I=P(1+(r)/(n))^(nt)-P \\ I=12000(1+(0.08)/(1))^(1\cdot4)-12000 \\ I=12000(1+0.08)^4-12000 \\ I=12000(1.08)^4-12000 \\ I=12000\cdot1.36048\ldots-12000 \\ I=16325.867\ldots-12000 \\ I=4325.867\ldots\approx4325.87 \end{gathered}`

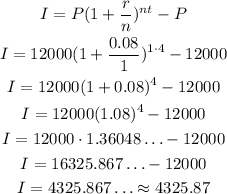
So, the interest amount is approximately $4,325.87.